Description
Why do we use the Pythagorean theorem?
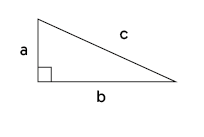
Mathematics helps us better understand the world around us. The Pythagorean theorem is a formula from mathematics, an important principle in geometry that deals with right-angled triangles. The theorem looks like this: 𝑎2+𝑏2=𝑐2a2+b2=c2
The letters 𝑎a, 𝑏b, and 𝑐c each represent one side of a triangle. In other words, they represent the lengths of the sides of the three squares that intersect each other on the exhibit board. The theorem states that the area of square 𝑎a plus the area of square 𝑏b together are exactly equal to the area of square 𝑐c. This means that if you know the length of side 𝑎a and the length of side 𝑏b, you can calculate the length of side 𝑐c. By rotating the disk, you can see how the content of two smaller compartments together fits exactly into a larger compartment.
The Pythagorean theorem is important everywhere angles play a role. So, in making toys (blocks) and in architecture (constructing structures). But also in surveying land for planning roads, in making machines, in calculating fast routes for transportation: everywhere, the Pythagorean theorem is used for calculating distances.
How does the Pythagorean theorem work?
- Rotate the disc until the large square is completely filled.
- Then, turn the disc and fill the smaller squares. What do you notice?


